Immortal numbers

Last update: 15 March 2024

The immortal numbers (Recreational mathematics) were defined and researched by Daniel Marschall and are defined as integers, which contain themselves as suffix when raised to a power.

Table of contents

• 1. Definitions
  • 1.0 Digit count function
  • 1.1 Simple case (base 10, power 2)
  • 1.2 General case (base b, power p)
  • 1.3 Set of immortal numbers
  • 1.4 Immortality of base/power-tuples
  • 1.5 Pseudo immortal base/power-tuples
  • 1.6 Super immortal numbers
• 2. Branch graph notation
• 3. Immortal number search
  • 3.1 Base 10, power 2
  • 3.2 Base b, power p
  • 3.3 Calculation using Chinese Remainder Theorem (power 2)
• 4. Graphical plots
  • 4.1 Immortal number overview
  • 4.2 Immortality of various (b,p)-tuples
  • 4.3 Pseudo immortal base/power tuples
• 5. Miscellaneous proofs, theorems and attributes
  • 5.1 An immortal number with power p is also immortal with power p+k(p-1)
  • 5.2 Theorem of complete immortality
  • 5.3 The only super-immortals are 0 and 1
  • 5.4 Only 0 and 1 are immortal to a base which has only one unique prime in its integer factorization (power 2)
• 6. Extension with complex numbers
  • 6.1 General case (base b, power p) with complex numbers
  • 6.2 Complex immortality of base/power-tuples
  • 6.3 Complex immortal number search
  • 6.4 Proof that (k+ki) is not immortal with power 2 for k ≠ 0 at any base b
• 7. Hypercomplex numbers
  • 7.0 General case for all complex and hypercomplex numbers
  • 7.1 Quaternions
    • 7.1.1 General case (base b, power p) with Quaternions
    • 7.1.2 Quaternion immortality of base/power-tuples
    • 7.1.3 Quaternion immortal number search
  • 7.2 Octonions
    • 7.2.1 General case (base b, power p) with Octonions
    • 7.2.2 Octonions immortality of base/power-tuples
    • 7.2.3 Octonions immortal number search
  • 7.3 Sedenions
    • 7.3.1 General case (base b, power p) with Sedenions
    • 7.3.2 Sedenions immortality of base/power-tuples
    • 7.3.3 Sedenions immortal number search
  • 7.4 Dual Numbers
    • 7.4.1 General case (base b, power p) with Dual Numbers
    • 7.4.2 Dual Numbers immortality of base/power-tuples
    • 7.4.3 Dual Numbers immortal number search
  • 7.5 Split Complex Numbers
    • 7.5.1 General case (base b, power p) with Split Complex Numbers
    • 7.5.2 Split Complex Numbers immortality of base/power-tuples
    • 7.5.3 Split Complex Numbers immortal number search
  • 7.6 Other Hypercomplex Number Systems
• 8. Alternative immortal numbers
• 9. Open questions and unproven theorems

1. Definitions

1.0 Digit count function

In this document we use the following function that counts the amount of digits of an integer $n\in \mathbb{Z}$, represented in base $b\in \mathbb{N}\setminus \{0,1\}$:

${\mathrm{{\rm Y}}}_b(n)=\lfloor {\log }_b(\mid n\mid )+1\rfloor$

1.1 Simple case (base 10, power 2)

Definition: A number $n\in {\mathbb{N}}_0$ is "immortal" (with power 2 at base 10), if it satisfies the following equation:

$n^2\equiv n\left(mod{\mathrm{\hspace{0.33em}10}}^{{\mathrm{{\rm Y}}}_{10}\left(n\right)}\right)$

Example: The number 625 is immortal at base 10, because 625 x 625 = 390625

1.2 General case (base b, power p)

Definition: A number $n\in {\mathbb{N}}_0$ is "immortal" with power $p\in \mathbb{N}\setminus \{0,1\}$ at base $b\in \mathbb{N}\setminus \{0,1\}$, if it satisfies the following equation:

$n^p\equiv n\left(mod{b}^{{\mathrm{{\rm Y}}}_b\left(n\right)}\right)$

Example: The number 2047 ( 3777₍₈₎ ) is immortal with power 3 at base 8, because 3777₍₈₎³ = 77720013777₍₈₎

A more general case with complex numbers and negative numbers can be found here.

1.3 Set of immortal numbers

The set ${𝕄}_b^p$ contains all immortal numbers with power $p$ at base $b$.

Definition:

$n\in \left({𝕄}_b^p\cap {\mathbb{N}}_0\right)\iff n^p\equiv n\left(mod{b}^{{\mathrm{{\rm Y}}}_b\left(n\right)}\right)$

Example: $625\in {𝕄}_{10}^2$

1.4 Immortality of base/power-tuples

The "immortality" of a ${𝕄}_b^p$ tuple is defined by the amount of immortal numbers divided by the maximum length of these numbers. The higher the maximum length is chosen, the more accurate is the immortality. The unit of measurement can be optionally written as $\frac{I}{D}$ ("Immortals per Digit"). Since the numbers $\{0,1\}$ are always immortal, they will be exluded from this calculation.

Formal definition:

Example 1: For base 10, power 2, there are 8 immortal numbers with length of 1-3 digits, excluding the super immortal numbers $0$ and $1$. The immortality of ${𝕄}_{10}^2$ is therefore ${|{𝕄}_{10}^3|}^{\mathbb{N}}\approx \frac{6}{3}=2$. Actually, we know that 2 is the exact value, since 2 is the amount of branches that exists for base 10, power 2.

Example 2: For base 10, power 3, there are 1176 immortal numbers with length of 1-100 digits, excluding the super immortal numbers $0$ and $1$. The immortality of ${𝕄}_{10}^3$ is therefore approximately ${|{𝕄}_{10}^3|}^{\mathbb{N}}\approx \frac{1176}{100}=11.76$

If you include negative numbers:

${\left|{𝕄}_b^p\right|}^{\mathbb{Z}}=2\cdot {\left|{𝕄}_b^p\right|}^{\mathbb{N}}$

Here you can find a plot that compares the immortality of various $(b,p)$ tuples.

A more general case with complex numbers and negative numbers can be found here.

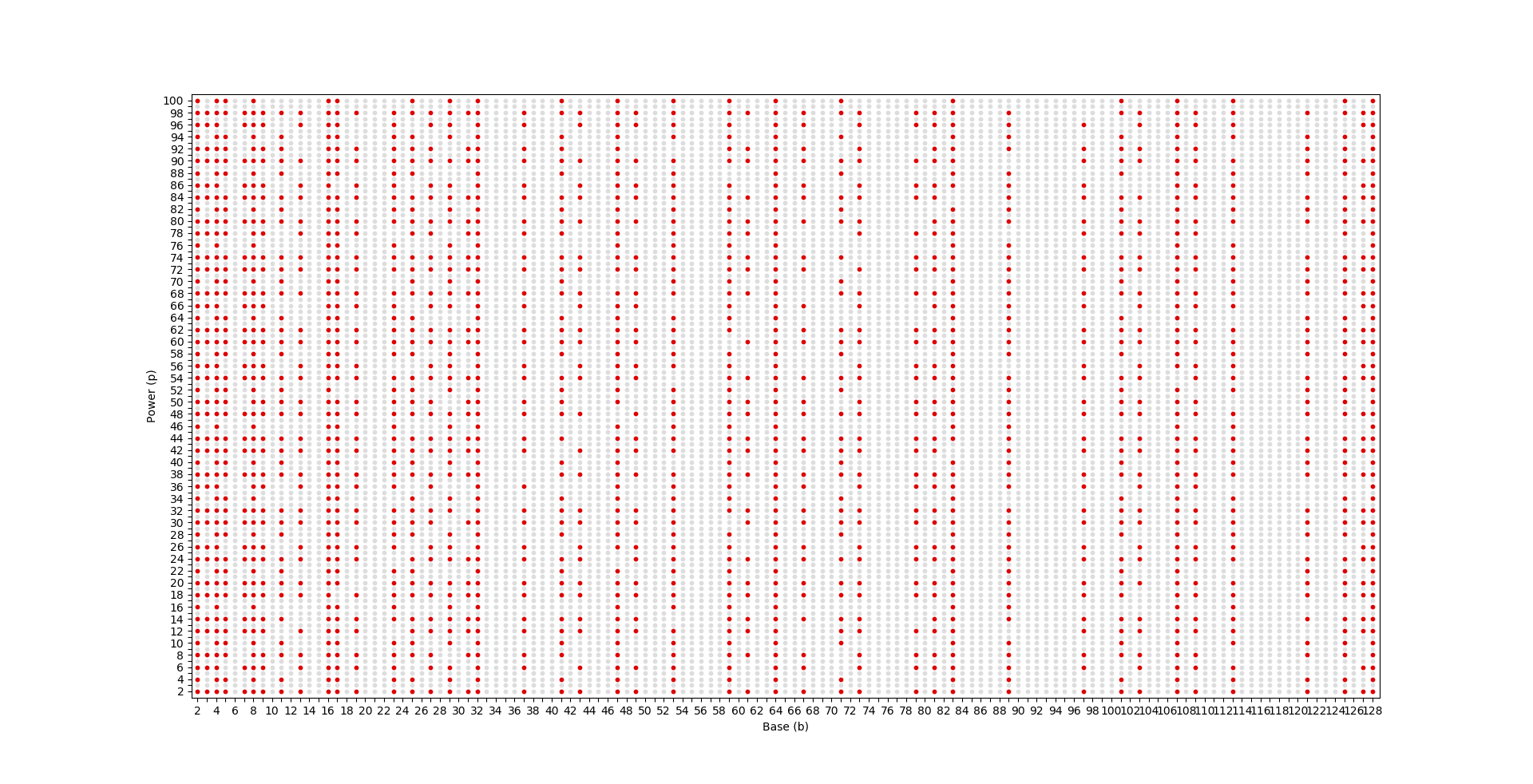
1.5 Pseudo immortal base/power-tuples

There are base/power-tuples $(b,p)$ where only the numbers ${𝕄}_b^p=\{0,1\}$ are immortal. These base/power-tuples are called "pseudo-immortal". An example is ${𝕄}_9^2$.

Their immortality is zero ${|{𝕄}_b^p|}^{\mathbb{N}}=0$ because:

Here you can find a plot that shows the $(b,p)$ tuples of some pseudo-immortals.

1.6 Super immortal numbers

Super immortal numbers are numbers which are immortal to every $(b,p)$ tuple. Only the numbers $\{0,1\}$ satisfy this property (see proof).

${𝕄}_s:=\bigcap _{b=2}^{\mathrm{\infty }}\bigcap _{p=2}^{\mathrm{\infty }}{𝕄}_b^p=\{0,1\}$

2. Branch graph notation

Immortal numbers can be written in graph with "branches".

In base 10, power 2, things are quite easy: There are only 4 branches 0, 1, 5 and 6. The branches 0 and 1 are trivial branches and have no children.
In branch 5, the immortal numbers are 5, 25, 625, 90625, 890625, 2890625, 12890625, 212890625, 8212890625, ...
In branch 6, the immortal numbers are 6, 76, 376, 9376, 109376, 7109376, 87109376, 787109376, 1787109376, ...
In this case, immortal numbers of base 10 power 2 can be generated using a tree node and adding a single digit in front of it. Additionally, the sum of the pairs of digits below branch 5 and 6 always add up to 9.

However, there are more complex graphs, for example base 10, power 3:

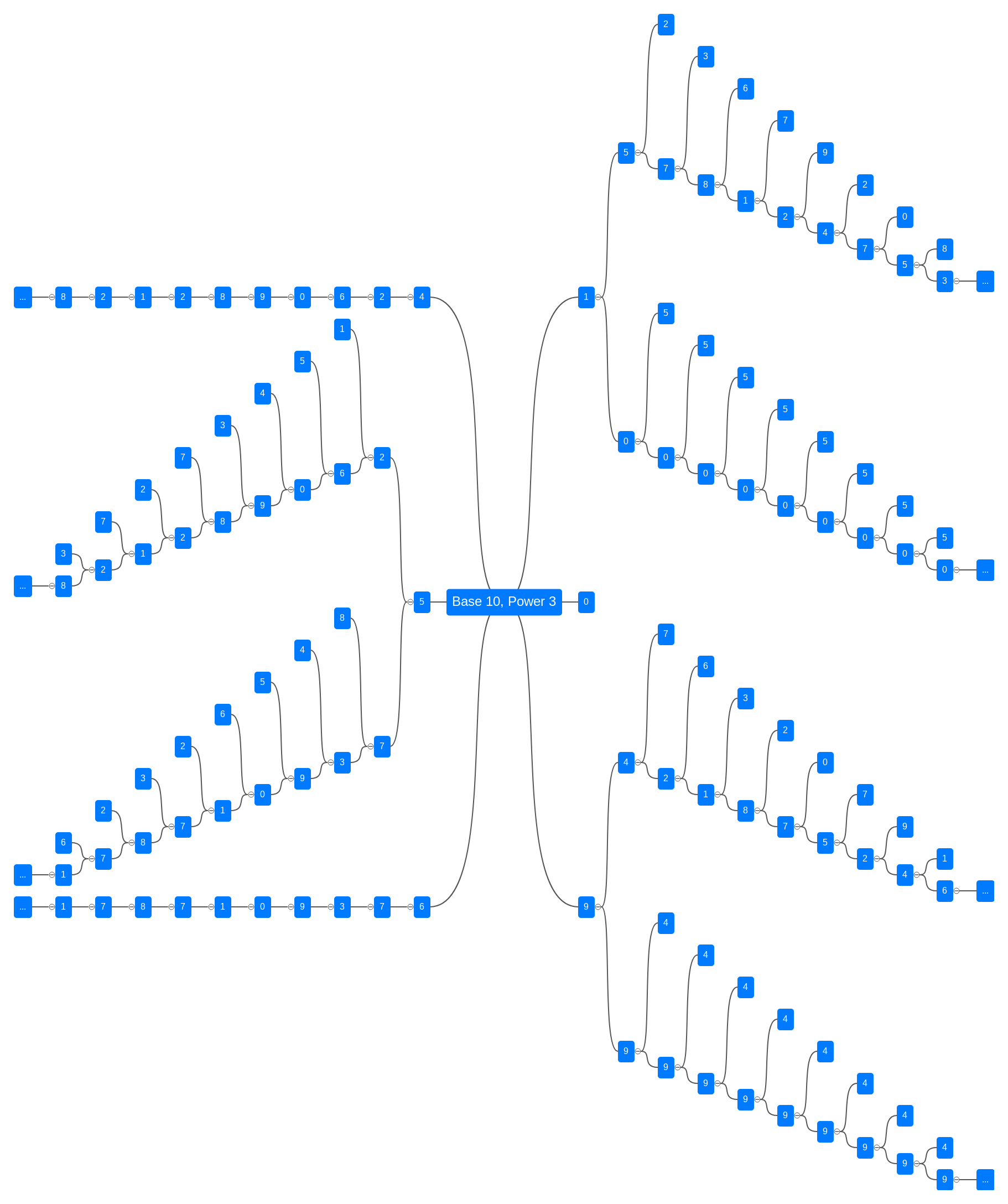
Credits: The graphs were created with mind-map-online.de

3. Immortal number search

3.1 Base 10, power 2

There has been a huge effort to find immortal numbers with several million digits. A special algorithm, optimized extensively using SSE/MMX technology, has been written to archive this task.

On July, 9th 2019, the immortal number of base 10, power 2 with 1.1 billion digits was found and on March, 30th 2020, the result was double-verified.

Download the giant immortal numbers:

• 1.1 billion digits long number of branch 5 (zipped, 493 MB)

• 1.1 billion digits long number of branch 6 (zipped, 493 MB)

• 1.1 billion digits raw data (reversed order), can be used to continue the calculation using the tool below (zipped, 508 MB)

• Statistics file created by the generation tool: initial run and verification run (both 3 MB)

Get the tool to calculate these numbers (Source codes written in C)

Credits: The search for giant immortal numbers at base-10-power-2 were only made possible by the users of the matheboard.de thread who contributed the algorithm for finding base-10-power-2 numbers as well as the contributor of this StackOverflow question who has showed me how to speed up the algorithm using SSE/MMX instructions.

3.2 Base b, power p

A rather trivial search algorithm has been developed to find all immortal numbers between base 2 and 36 and power 2 till 10, with a maximum length of 100 digits.

Python source code

Get a list of immortal numbers with max length 100 digits, for powers 2 till 10, with the following base:
02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

3.3 Calculation using Chinese Remainder Theorem (power 2)

4. Graphical plots

4.1 Immortal number overview

Python source code

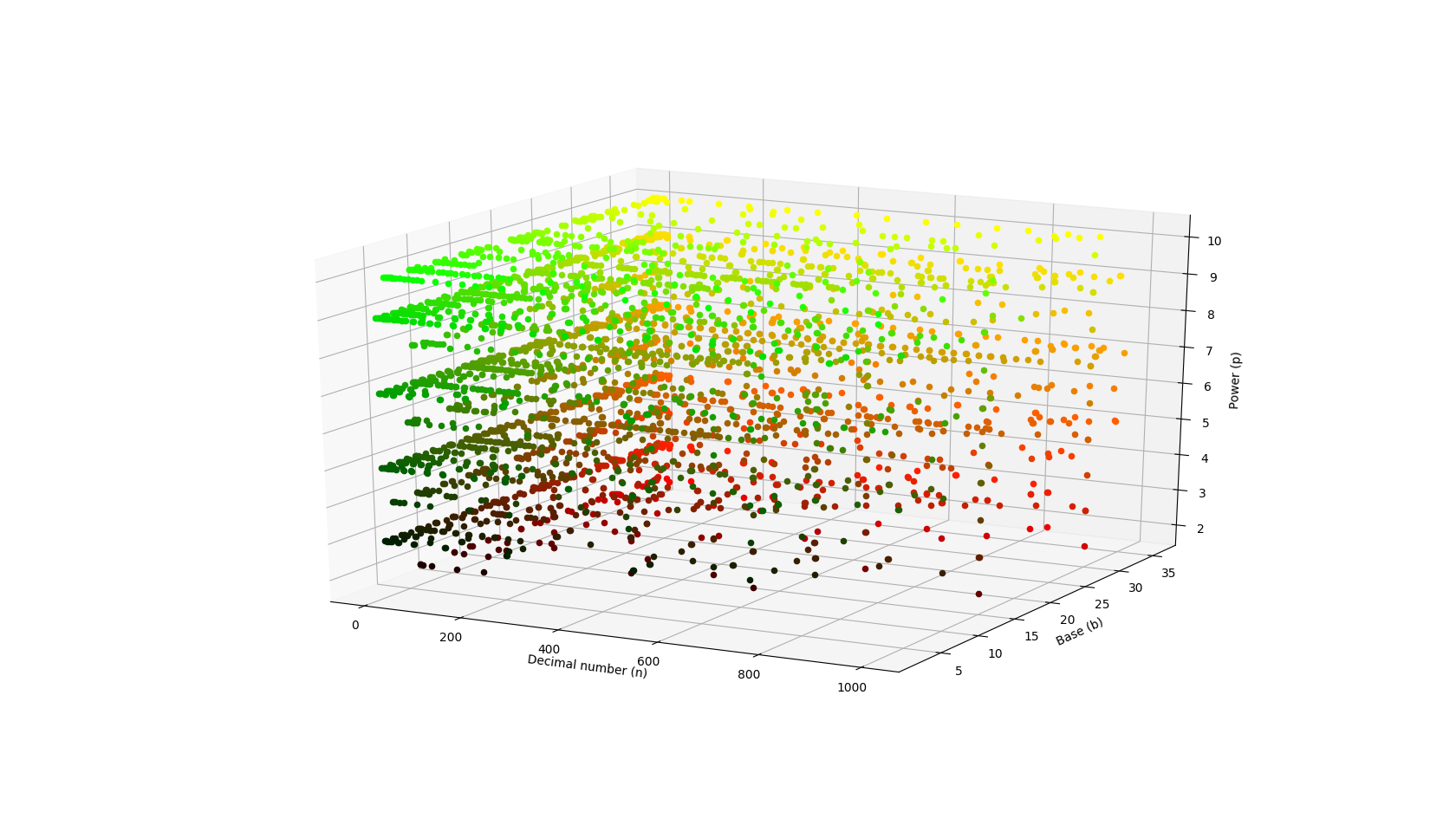
Base 10 filtered:

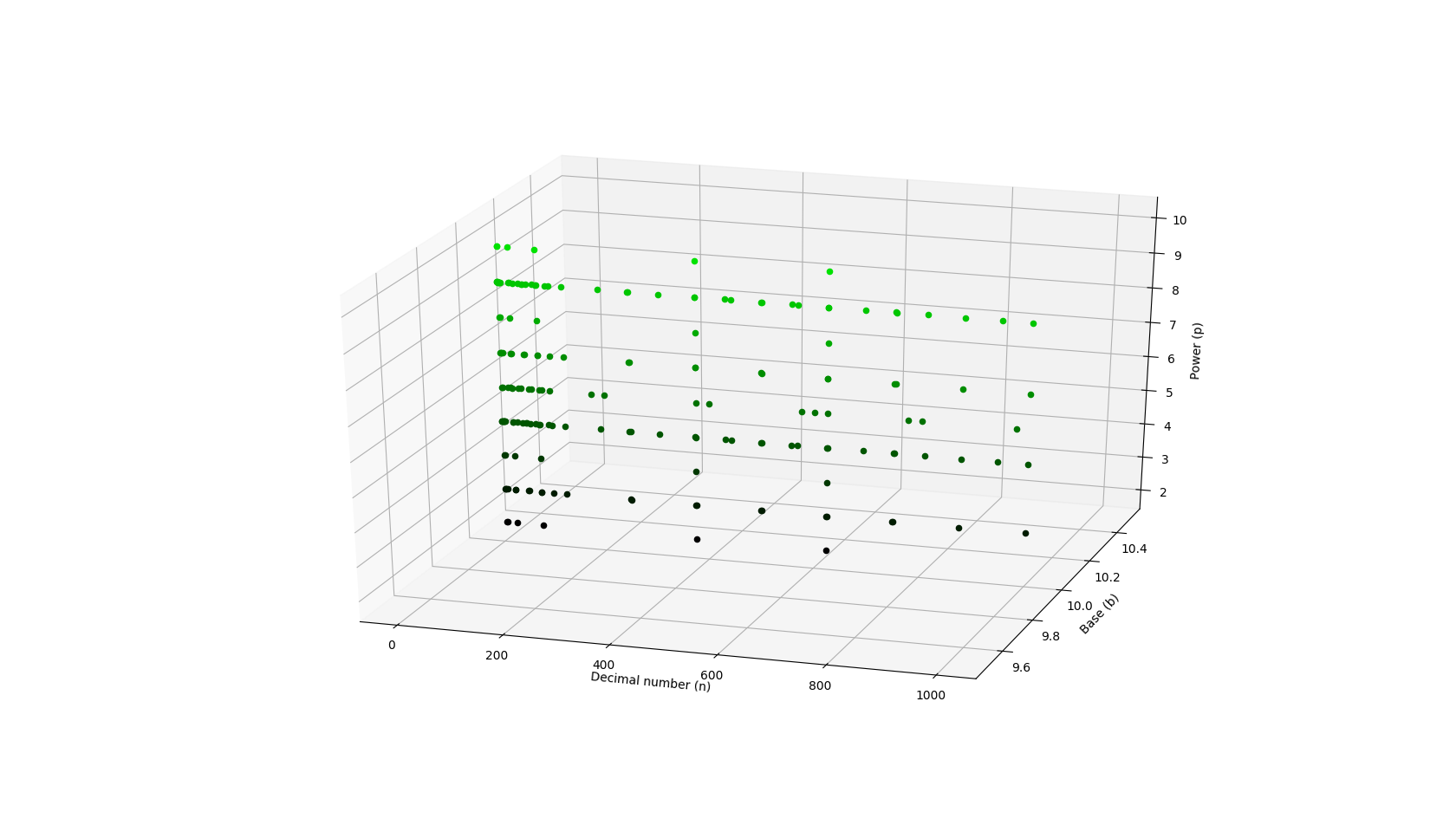
4.2 Immortality of various (b,p)-tuples

Python source code

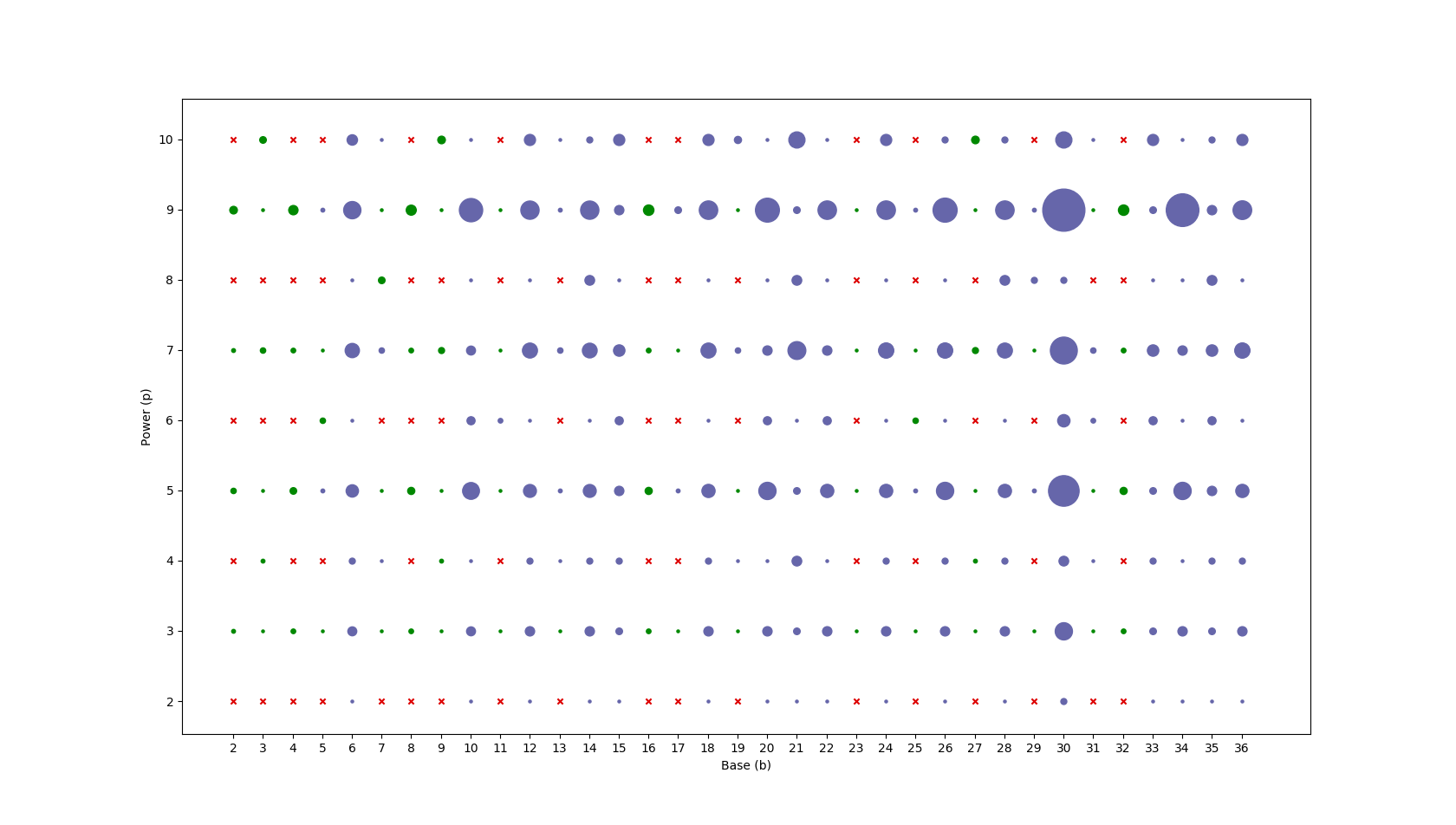
A red x denotes an immortality of zero. Dots denote an immortality. The bigger the dots are, the greater is the immortality of ${𝕄}_b^p$ .
Green dots denote an immortality of $\mathbb{N}$.
Blue dots denote an immortality of $ℝ$.

4.3 Pseudo immortal base/power tuples

Python source code

5. Miscellaneous proofs, theorems and attributes

5.1 An immortal number with power p is also immortal with power p+k(p-1)

We want to prove that ${𝕄}_b^p\subseteq {𝕄}_b^{p+k\left(p-1\right)},k\in {\mathbb{N}}_0$

Let's begin with:

$n\in ({𝕄}_b^p\cap \mathbb{N})\iff n^p\equiv n(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})|\cdot n^{p-1}$

$n^p\cdot n^{p-1}\equiv n\cdot n^{p-1}(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})$

$n^{p+p-1}\equiv n^{1+p-1}(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})$

$n^{p+(p-1)}\equiv n^p(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})$

With mathematical induction we can now prove that

$n^{p+k(p-1)}\equiv n^{p+(k-1)(p-1)}\equiv \mathrm{\dots }\equiv n^{p+(p-1)}\equiv n^p\equiv n(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})$

therefore

$n\in ({𝕄}_b^{p+k(p-1)}\cap \mathbb{N})\iff n\in ({𝕄}_b^{p+(k-1)(p-1)}\cap \mathbb{N})\iff \mathrm{\dots }\iff n\in {𝕄}_b^{p+(p-1)}\iff n\in ({𝕄}_b^p\cap \mathbb{N})$

Since all immortal numbers of power $p$ are also immortal in power $p+k(p-1)$, we have now proven that

${𝕄}_b^p\subseteq {𝕄}_b^{p+k\left(p-1\right)}\mathrm{■}$

5.2 Theorem of complete immortality

Theorem: For every number $n\in {\mathbb{N}}_0$ there is a tuple $(b,p)$ so that $n\in {𝕄}_b^p$. In other words, every number is immortal to some specific base and power.

$\forall n\in {\mathbb{N}}_0\exists (b,p):n\in {𝕄}_b^p$

Note: The theorem of complete immortality also leads to the conclusion:

$\bigcup _{b=2}^{\mathrm{\infty }}\bigcup _{p=2}^{\mathrm{\infty }}{𝕄}_b^p={\mathbb{N}}_0$

Proof:

(0) Let $n\in {\mathbb{N}}_0$ with an arbitary value.

(1) Let $b$ be a prime $b\in \mathbb{P}$ that is not a prime factor of $n$ ( $n\nmid b$ ), then $m:=b^{{\mathrm{{\rm Y}}}_b(n)}$ is not a prime factor of $n$ either ( $n\nmid m$ ).

In other words: $\gcd (b,n)=1\Rightarrow \gcd (m,n)=1$ .

(2) Since we have $\gcd (m,n)=1$, we can create the following term using the Fermat-Euler theorem:

$n^{\phi (m)}\equiv 1(modm)$

Transforming it a bit, we get:

$n^{\phi (m)}\equiv 1(modm)|\cdot n$

$n^{\phi (m)}\cdot n\equiv n(modm)$

$n^{\phi (m)+1}\equiv n(modm)$

(3) If we now define $p:=\phi (m)+1$ and insert the definition of $m$ from above, then we get:

$n^p\equiv n\left(mod{b}^{{\mathrm{{\rm Y}}}_b\left(n\right)}\right)$

which is equivalent to:

$n\in {𝕄}_b^p\mathrm{■}$

Credits: Many thanks to Finn from matheboard.de for showing me how to prove this theorem!

5.3 The only super-immortals are 0 and 1

We want to prove that the only super-immortals are 0 and 1.

${𝕄}_s:=\bigcap _{b=2}^{\mathrm{\infty }}\bigcap _{p=2}^{\mathrm{\infty }}{𝕄}_b^p=\{0,1\}$

(1) First, we verify that 0 and 1 are immortal to every $b,p\in \mathbb{N}\setminus \{0,1\}$ :

(1.1) $\forall b,p\ge 2:{\mathrm{\hspace{0.33em}0}}^p=0\Rightarrow 0^p\equiv 0(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})\Rightarrow 0\in {𝕄}_b^p$

(1.2) $\forall b,p\ge 2:{\mathrm{\hspace{0.33em}1}}^p=1\Rightarrow 1^p\equiv 1(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})\Rightarrow 1\in {𝕄}_b^p$

(2) To prove that the only super-immortals are 0 and 1, we want to find a $(b,p)$ tuple for every $n>1$ that will cause $n\notin {𝕄}_b^p$ :

$\forall n\in \mathbb{N}\setminus \{0,1\}\exists (b,p):n\notin {𝕄}_b^p;b,p\in \mathbb{N}\setminus \{0,1\}$

(3) The definition of an immortal number is

$n^p\equiv n(mod{b}^{{\mathrm{{\rm Y}}}_b(n)})$

We can see that a number can only be immortal if $n^p$ is a number that has more digits (in the notation of base $b$) than $n$.

(4) If we choose a high enough base $b$, then $n$ and $n^p$ would have the same amounts of digits, and therefore $n$ could not be immortal.

So, we need to find a $b$, so that $b^{{\mathrm{{\rm Y}}}_b(n)}>n^p$ .

If we choose $b:=n^p$, we get:

$n^{p^{{\mathrm{{\rm Y}}}_{(n^p)}(n)}}>n^p$

$n^{p^{\lfloor {\log }_{n^p}(n)+1\rfloor }}>n^p$

$n^{p+\lfloor {\log }_{n^p}(n)+1\rfloor }>n^p$

$n^{p+\lfloor \frac{\ln n}{\ln n^p}+1\rfloor }>n^p$

$n^{p+\lfloor \frac{\ln n}{p\cdot \ln n}+1\rfloor }>n^p$

$n^{p+\lfloor \frac{1}{p}+1\rfloor }>n^p$

$n^{p+\lfloor \frac{1}{p}\rfloor +1}>n^p$

If $p>1$, then $\lfloor \frac{1}{p}\rfloor =0$ and therefore:

$n^{p+0+1}>n^p$, which is true, if $n>1$.

(5) We continue by taking the general definition of an immortal number

$n^p\equiv n(mod{b}^{{\mathrm{{\rm Y}}}_b(n)});b,p\in \mathbb{N}\setminus \{0,1\}$

which can also be written as:

$(n^{p}mod{b}^{{\mathrm{{\rm Y}}}_b(n)})=(nmod{b}^{{\mathrm{{\rm Y}}}_b(n)})$

Since $b^{{\mathrm{{\rm Y}}}_b(n)}>n^p$ and $b^{{\mathrm{{\rm Y}}}_b(n)}>n$ ( because $n^p>n$ if $p\ge 2$ ) :

$(n^{p}mod{b}^{{\mathrm{{\rm Y}}}_b(n)})=(nmod{b}^{{\mathrm{{\rm Y}}}_b(n)})\Rightarrow n^p=n$, which is false if $p\ge 2$ .

Side note:
$(amodm):=a-\lfloor \frac{a}{m}\rfloor \cdot m$
If $m>a$ , then: $(amodm)=a-0\cdot m=a$

(6) Therefore:

$\forall n\in \mathbb{N}\setminus \{0,1\}:n\notin {𝕄}_{b:=n^p}^p,p\in \mathbb{N}\setminus \{0,1\}$

$\iff \forall n\in \mathbb{N}\setminus \{0,1\}:n\notin {𝕄}_s$

(7) Bringing together the results of step (1) and (6), we can conclude:

${𝕄}_s=\{0,1\}\mathrm{■}$

5.4 Only 0 and 1 are immortal to a base which has only one unique prime in its integer factorization (power 2)

Theorem:

If $b\in \mathbb{P}$ is prime, or the if the prime decomposition of $b$ consists only of a single prime,
then there are no immortal numbers except $\{0,1\}\in {𝕄}_b^2$.

$b=p_1^{}{}_{}{}^{n_1}\Rightarrow {𝕄}_b^2=\{0,1\}$

$p_1\in \mathbb{P},n_1\in {\mathbb{N}}_0$

Proof:

Since the prime decomposition only consists of a single product $p_1^{}{}_{}{}^{n_1}$,
there is just one congruence equation (see Solution via Chinese Remainder Theorem above):

$x\equiv a_1(mod{(p_1^{}{}_{}{}^{n_1})}^m)$

with $a_1=\{0,1\}$ and $m\in \mathbb{N}$ being the length of $x$.

Therefore, the solutions of $x$ are $\{0,1\}\mathrm{■}$

6. Extension with complex numbers

6.1 General case (base b, power p) with complex numbers

Definition: A complex number $z\in \{ℂ\mid \mathrm{\Re }(z)\in \mathbb{Z}\wedge \mathrm{\Im }(z)\in \mathbb{Z}\}$ is "immortal" with power $p\in \mathbb{N}\setminus \{0,1\}$ at base $b\in \mathbb{N}\setminus \{0,1\}$, if it satisfies the following equation:

$\begin{array}{c}\hfill z\in \left({𝕄}_b^p\cap ℂ\right)\iff \\ \hfill |\mathrm{\Re }(z^p)|\equiv |\mathrm{\Re }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Re }(z))})\wedge \\ \hfill |\mathrm{\Im }(z^p)|\equiv |\mathrm{\Im }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Im }(z))})\end{array}$

This general case also allows negative numbers, e.g. $(-313+216\mathrm{i})$ is immortal with base 10 and power 2, because (-313+216i)² = (51313-135216i).

6.2 Complex immortality of base/power-tuples

The "complex immortality" of a $(b,p)$ tuple is defined by the amount of positive complex immortal numbers divided by the maximum length of the imaginary and real part of these complex numbers raised to the cardinality of the set. The higher the maximum length is chosen, the more accurate is the immortality. The unit of measurement can be optionally written as $\frac{I}{D}$ ("Immortals per Digit"). Since the numbers $\{(0+0\mathrm{i}),(1+0\mathrm{i})\}$ are always immortal, they will be exluded from this calculation.

Formal definition:

When all components are positive:

When negative numbers are allowed:

Example: For base 10, power 2, there are 27 immortal complex numbers (10 without imaginary part and 17 with imaginary part) with imaginary/real part with length of 1-5 digits, excluding the super immortal numbers $(0+0\mathrm{i})$ and $(1+0\mathrm{i})$. The complex immortality of ${𝕄}_{10}^2$ with only positive components is allowed is therefore approximately ${|{𝕄}_{10}^2|}^{{ℂ}^{+}}\approx \frac{27}{5^2}=1.08$.
In comparison, the non-complex immortality (natural numbers $\mathbb{N}$) for base 2, power 10, with 1-5 digits is: ${|{𝕄}_{10}^2|}^{\mathbb{N}}\approx \frac{10}{5}=2$.

6.3 Complex immortal number search

See a list of 1700 found immortal numbers with non-zero imaginary part here

Source code can be found here

6.4 Proof that (k+ki) is not immortal with power 2 for k ≠ 0 at any base b

Let $z:=(x+yi)$.

$\begin{array}{c}\hfill z\in ({𝕄}_b^2\cap ℂ)\iff \\ \hfill |\mathrm{\Re }(z^2)|\equiv |\mathrm{\Re }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Re }(z))})\wedge \\ \hfill |\mathrm{\Im }(z^2)|\equiv |\mathrm{\Im }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Im }(z))})\iff \\ \hfill |x^2-y^2|\equiv |x|(mod{b}^{{\mathrm{{\rm Y}}}_b(x)})\wedge \\ \hfill |2xy|\equiv |y|(mod{b}^{{\mathrm{{\rm Y}}}_b(y)}),\\ \hfill x\in \mathbb{Z},y\in \mathbb{Z}\end{array}$

Assume $x=y\Rightarrow \mathrm{\Re }(z^2)=x^2-y^2=0,0\not\equiv \mid x\mid (mod{b}^{{\mathrm{{\rm Y}}}_b(x)})\forall x>0$.

Therefore, $x$ can only be 0.

Then, $y$ can only be 0, too, due to our previous assumption $x=y$ and additionally because $x=0\Rightarrow \mathrm{\Im }(z^2)=2xy=0,0\not\equiv |y|(mod{b}^{{\mathrm{{\rm Y}}}_b(y)})\forall y>0$.

So, the only possibility is $x=y=0\Rightarrow {(0+0\mathrm{i})}^2=(0+0\mathrm{i})\mathrm{■}$

7. Hypercomplex numbers

7.0 General case for all complex and hypercomplex numbers

General rule for all complex and hypercomplex number systems $S$:

Definition: $z\in \{S\mid \mathrm{\Re }(z)\in \mathbb{Z}\wedge \mathrm{\Im }(z)\in {\mathbb{Z}}^{{\dim }_{ℝ}(S)-1}\}$ is "immortal" with power $p\in \mathbb{N}\setminus \{0,1\}$ at base $b\in \mathbb{N}\setminus \{0,1\}$, if it satisfies the following equation:

$\begin{array}{c}\hfill z\in \left({𝕄}_b^p\cap S\right)\iff \\ \hfill |\mathrm{\Re }(z^p)|\equiv |\mathrm{\Re }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Re }(z))})\wedge \\ \hfill {\wedge }_{i=1}^{{\dim }_{ℝ}(S)-1}|{\mathrm{\Im }}_i(z^p)|\equiv |{\mathrm{\Im }}_i(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b({\mathrm{\Im }}_i(z))})\end{array}$

where ${\mathrm{{\rm Y}}}_b(n)$ is the digit count function and ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)$, starting with $i=1$.

Definition: The "immortality" when all components are positive is:

where ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)$, starting with $i=1$.

Definition: The "immortality" when negative numbers are allowed is:

where ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)$, starting with $i=1$.

7.1 Quaternions

7.1.1 General case (base b, power p) with Quaternions

Definition: A Quaternion $z\in \{ℍ\mid \mathrm{\Re }(z)\in \mathbb{Z}\wedge \mathrm{\Im }(z)\in {\mathbb{Z}}^3\}$ is "immortal" with power $p\in \mathbb{N}\setminus \{0,1\}$ at base $b\in \mathbb{N}\setminus \{0,1\}$, if it satisfies the following equation:

$\begin{array}{c}\hfill z\in \left({𝕄}_b^p\cap ℍ\right)\iff \\ \hfill |\mathrm{\Re }(z^p)|\equiv |\mathrm{\Re }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Re }(z))})\wedge \\ \hfill {\wedge }_{i=1}^{{\dim }_{ℝ}(ℍ)-1}|{\mathrm{\Im }}_i(z^p)|\equiv |{\mathrm{\Im }}_i(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b({\mathrm{\Im }}_i(z))})\end{array}$

where ${\mathrm{{\rm Y}}}_b(n)$ is the digit count function and ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)\in {\mathbb{Z}}^3$, starting with $i=1$.

Example: $(93+2\mathrm{i}+4\mathrm{j}+6\mathrm{k})$ is immortal with base 10 and power 2, because (93+2i+4j+6k)² = (8593+372i+744j+1116k).

This general case also allows negative numbers.

7.1.2 Quaternion immortality of base/power-tuples

Quaternion immortality follows the same scheme as the complex immortality.

When all components are positive:

where ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)\in {\mathbb{Z}}^3$, starting with $i=1$.

When negative numbers are allowed:

where ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)\in {\mathbb{Z}}^3$, starting with $i=1$.

Approximation for various powers at base 10, using quaternions with 1-2 digits and only positive components;
2 is subtracted from the amount of integers in order to exclude the super immortal numbers 0 and 1:

${|{𝕄}_{10}^{power}|}^{{ℍ}^{+}}\approx \frac{truequaternionnumbers+purecomplexnumbers+integers-2}{2^4}$

${|{𝕄}_{10}^2|}^{{ℍ}^{+}}\approx \frac{1432+4+6-2}{2^4}=90$

${|{𝕄}_{10}^3|}^{{ℍ}^{+}}\approx \frac{5773+96+13-2}{2^4}=367.5$

${|{𝕄}_{10}^4|}^{{ℍ}^{+}}\approx \frac{3769+17+6-2}{2^4}=236.875$

${|{𝕄}_{10}^5|}^{{ℍ}^{+}}\approx \frac{797580+243+22-2}{2^4}=49865.1875$

${|{𝕄}_{10}^6|}^{{ℍ}^{+}}\approx \frac{5166+34+14-2}{2^4}=325.75$

${|{𝕄}_{10}^7|}^{{ℍ}^{+}}\approx \frac{188034+100+13-2}{2^4}=11759.0625$

${|{𝕄}_{10}^8|}^{{ℍ}^{+}}\approx \frac{3232+8+6-2}{2^4}=202.75$

${|{𝕄}_{10}^9|}^{{ℍ}^{+}}\approx \frac{999125+274+22-2}{2^4}=62463.6875$

${|{𝕄}_{10}^{10}|}^{{ℍ}^{+}}\approx \frac{1856+7+6-2}{2^4}=116.6875$

7.1.3 Quaternion immortal number search

Only a very short search for Quaternion immortal numbers has been done with only 1-2 digits and powers 2 and 3.

Source code and results can be found here

7.2 Octonions

7.2.1 General case (base b, power p) with Octonions

Definition: An Octonion $z\in \{𝕆\mid \mathrm{\Re }(z)\in \mathbb{Z}\wedge \mathrm{\Im }(z)\in {\mathbb{Z}}^7\}$ is "immortal" with power $p\in \mathbb{N}\setminus \{0,1\}$ at base $b\in \mathbb{N}\setminus \{0,1\}$, if it satisfies the following equation:

$\begin{array}{c}\hfill z\in \left({𝕄}_b^p\cap 𝕆\right)\iff \\ \hfill |\mathrm{\Re }(z^p)|\equiv |\mathrm{\Re }(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b(\mathrm{\Re }(z))})\wedge \\ \hfill {\wedge }_{i=1}^{{\dim }_{ℝ}(𝕆)-1}|{\mathrm{\Im }}_i(z^p)|\equiv |{\mathrm{\Im }}_i(z)|(mod{b}^{{\mathrm{{\rm Y}}}_b({\mathrm{\Im }}_i(z))})\end{array}$

where ${\mathrm{{\rm Y}}}_b(n)$ is the digit count function and ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)\in {\mathbb{Z}}^7$, starting with $i=1$.

Example: $(3e_0+0e_1+4e_2+6e_3+4e_4+4e_5+2e_6+2e_7)$ is immortal with base 10 and power 2,
because (3e₀ + 0e₁ + 4e₂ + 6e₃ + 4e₄ + 4e₅ + 2e₆ + 2e₇)² = (-83e₀ + 0e₁ + 24e₂ + 36e₃ + 24e₄ + 24e₅ + 12e₆ + 12e₇).

This general case also allows negative numbers.

7.2.2 Octonions immortality of base/power-tuples

Formal definition:

When all components are positive:

where ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)\in {\mathbb{Z}}^7$, starting with $i=1$.

When negative numbers are allowed:

where ${\mathrm{\Im }}_i(z)$ is the $i$-th element of the vector $\mathrm{\Im }(z)\in {\mathbb{Z}}^7$, starting with $i=1$.

Approximation for various powers at base 10, using immortal Octonions with 1 digit and only positive parts;
2 is subtracted from the amount of integers in order to exclude the super immortal numbers 0 and 1:

${|{𝕄}_{10}^{power}|}^{{𝕆}^{+}}\approx \frac{trueoctonions+purequaternions+complexnumbers+integers-2}{1^8}$

${|{𝕄}_{10}^2|}^{{𝕆}^{+}}\approx \frac{31144+43+2+4-2}{1^8}=31191$

${|{𝕄}_{10}^3|}^{{𝕆}^{+}}\approx \frac{5294719+592+17+6-2}{1^8}=5295332$

${|{𝕄}_{10}^4|}^{{𝕆}^{+}}\approx \frac{51436+85+1+4-2}{1^8}=51524$

${|{𝕄}_{10}^5|}^{{𝕆}^{+}}\approx \frac{19083133+1638+23+10-2}{1^8}=19084802$

${|{𝕄}_{10}^6|}^{{𝕆}^{+}}\approx \frac{24360+40+2+4-2}{1^8}=24404$

${|{𝕄}_{10}^7|}^{{𝕆}^{+}}\approx \frac{6840142+766+21+6-2}{1^8}=6840933$

${|{𝕄}_{10}^8|}^{{𝕆}^{+}}\approx \frac{32399+53+3+4-2}{1^8}=32457$